题目列表
HDU:1232
HDU 1232 畅通工程
Description
某省调查城镇交通状况,得到现有城镇道路统计表,表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通(但不一定有直接的道路相连,只要互相间接通过道路可达即可)。问最少还需要建设多少条道路?
Input
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是城镇数目N ( < 1000 )和道路数目M;随后的M行对应M条道路,每行给出一对正整数,分别是该条道路直接连通的两个城镇的编号。为简单起见,城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时,输入结束,该用例不被处理。
Output
对每个测试用例,在1行里输出最少还需要建设的道路数目。
Sample Input
4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0
Sample Output
1
0
2
998
Hint
Huge input, scanf is recommended.
解题思路
要求的是输出最少需要建设的条数,一共给出了N个点,那么如果一条路也没有的话,最少就需要建立N - 1条路,也就是先把最后的结论ans初始化为N - 1。然后,针对每输入的一对点,判断这两个点的父亲,如果不相等的话,证明这两个城市没有办法联通,需要建路,那么此时的ans就应该减1,依次处理到最后一组数据。最后ans就是题目的答案。
AC代码
31MS/1412K/G++1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const int N = 1005;
int father[N], ans = 0;
int findset(int x)
{
return father[x] == x ? x : father[x] = findset(father[x]);
}
void unionset(int a, int b)
{
a = findset(a);
b = findset(b);
if (a != b)
{
ans--;
father[a] = b;
}
}
int main()
{
int n, m;
while (~scanf("%d", &n) && n)
{
scanf("%d", &m);
for (int i = 1; i <= n; i++)
{
father[i] = i;
}
int a, b;
ans = n - 1;
for (int i = 1; i <= m; i++)
{
scanf("%d%d", &a, &b);
unionset(a, b);
}
printf("%d\n", ans);
}
return 0;
}
POJ 1308 Is It A Tree?
Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.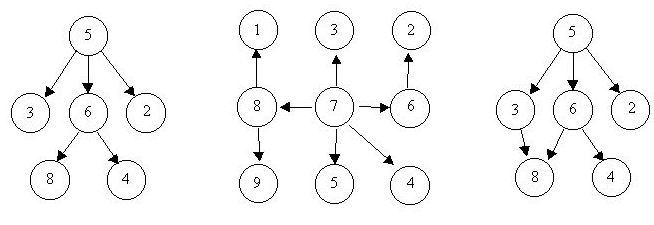
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line “Case k is a tree.” or the line “Case k is not a tree.”, where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
解题思路
需要判断几种不是树的情况:
- 0 0 空树是一棵树
- 1 1 0 0 不是树 不能自己指向自己
- 1 2 1 3 2 3 0 0 成环不是树
- 1 2 2 3 4 5 森林不算是树(主要是注意自己)
综上也就是三种大情况,全都讨论了就没问题了。
AC代码
172K/0MS/C++1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
const int N = 1005;
int father[N], flag[N];
void init()
{
for (int i = 0; i <= 1000; i++)
{
father[i] = i;
flag[i] = false;
}
}
int findset(int x)
{
return father[x] == x ? x : father[x] = findset(father[x]);
}
void unionset(int a, int b)
{
a = findset(a);
b = findset(b);
if (a != b) father[a] = b;
}
int main()
{
int x, y, t = 1, first;
while (~scanf("%d%d", &x, &y))
{
if (x == -1 && y == -1) break;
//空树是一棵树
if (x == 0 && y == 0)
{
printf("Case %d is a tree.\n", t++);
continue;
}
init();
flag[x] = flag[y] = true;
first = x;
bool tree = true;
//同if (findset(x) == findset(y))
if (x == y) tree = false;
else unionset(x, y);
while (~scanf("%d%d", &x, &y) && x + y)
{
flag[x] = flag[y] = true;
//不能为环
if (findset(x) == findset(y)) tree = false;
unionset(x, y);
}
int root = findset(first);
//不能为森林
for (int i = 1; i <= 1000; i++)
{
if (flag[i] && findset(i) != root)
tree = false;
}
if (tree) printf("Case %d is a tree.\n", t++);
else printf("Case %d is not a tree.\n", t++);
}
return 0;
}
POJ 1611 The Suspects
Description
Severe acute respiratory syndrome (SARS), an atypical pneumonia of unknown aetiology, was recognized as a global threat in mid-March 2003. To minimize transmission to others, the best strategy is to separate the suspects from others.
In the Not-Spreading-Your-Sickness University (NSYSU), there are many student groups. Students in the same group intercommunicate with each other frequently, and a student may join several groups. To prevent the possible transmissions of SARS, the NSYSU collects the member lists of all student groups, and makes the following rule in their standard operation procedure (SOP).
Once a member in a group is a suspect, all members in the group are suspects.
However, they find that it is not easy to identify all the suspects when a student is recognized as a suspect. Your job is to write a program which finds all the suspects.
Input
The input file contains several cases. Each test case begins with two integers n and m in a line, where n is the number of students, and m is the number of groups. You may assume that 0 < n <= 30000 and 0 <= m <= 500. Every student is numbered by a unique integer between 0 and n−1, and initially student 0 is recognized as a suspect in all the cases. This line is followed by m member lists of the groups, one line per group. Each line begins with an integer k by itself representing the number of members in the group. Following the number of members, there are k integers representing the students in this group. All the integers in a line are separated by at least one space.
A case with n = 0 and m = 0 indicates the end of the input, and need not be processed.
Output
For each case, output the number of suspects in one line.
Sample Input
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2
200 2
1 5
5 1 2 3 4 5
1 0
0 0
Sample Output
4
1
1
解题思路
需要使用一个num[x]来记录每一个父亲节点所包含的子节点数量,创建集合的时候每一个社团里的人都与该社团的第一个人连接,这样每个社团就能组成一个集合了。最后判断0属于哪个集合,输出num[findset(0)]即可。
AC代码
400K/16MS/C++1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
const int N = 30005;
int father[N], num[N];
void init()
{
for (int i = 0; i <= 30000; i++)
{
father[i] = i;
num[i] = 1;
}
}
int findset(int x)
{
return father[x] == x ? x : father[x] = findset(father[x]);
}
void unionset(int a, int b)
{
a = findset(a);
b = findset(b);
if (a != b)
{
father[a] = b;
num[b] += num[a];
}
}
int main()
{
int n, m, k, a, b;
while (~scanf("%d%d", &n, &m) && n + m)
{
init();
for (int i = 1; i <= m; i++)
{
scanf("%d", &k);
scanf("%d", &a);
for (int i = 1; i < k; i++)
{
scanf("%d", &b);
unionset(a, b);
}
}
printf("%d\n", num[findset(0)]);
}
return 0;
}
POJ 1703 Find them, Catch them
Description
The police office in Tadu City decides to say ends to the chaos, as launch actions to root up the TWO gangs in the city, Gang Dragon and Gang Snake. However, the police first needs to identify which gang a criminal belongs to. The present question is, given two criminals; do they belong to a same clan? You must give your judgment based on incomplete information. (Since the gangsters are always acting secretly.)
Assume N (N <= 10^5) criminals are currently in Tadu City, numbered from 1 to N. And of course, at least one of them belongs to Gang Dragon, and the same for Gang Snake. You will be given M (M <= 10^5) messages in sequence, which are in the following two kinds:
D [a] [b]
where [a] and [b] are the numbers of two criminals, and they belong to different gangs.A [a] [b]
where [a] and [b] are the numbers of two criminals. This requires you to decide whether a and b belong to a same gang.
Input
The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case begins with a line with two integers N and M, followed by M lines each containing one message as described above.
Output
For each message “A [a] [b]” in each case, your program should give the judgment based on the information got before. The answers might be one of “In the same gang.”, “In different gangs.” and “Not sure yet.”
Sample Input
1
5 5
A 1 2
D 1 2
A 1 2
D 2 4
A 1 4
Sample Output
Not sure yet.
In different gangs.
In the same gang.
解题思路
使用num[x]数组记录和x敌对的人的编号,建立集合的时候,将x的敌对方num[x]和y建立到一起,这两拨人才是属于同一个集合的,最后判断,输出结论就好。
AC代码
948K/329MS/C++1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
const int N = 100005;
int father[N], num[N]; //num[x]表示x的敌对势力
void init()
{
for (int i = 0; i <= 100000; i++)
{
father[i] = i;
//没有敌对势力
num[i] = 0;
}
}
int findset(int x)
{
return father[x] == x ? x : father[x] = findset(father[x]);
}
void unionset(int a, int b)
{
a = findset(a);
b = findset(b);
if (a != b) father[a] = b;
}
int main()
{
int t, a, b, m, n;
char c;
scanf("%d", &t);
while (t--)
{
init();
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
{
scanf(" %c%d%d", &c, &a, &b);
if (c == 'D')
{
if (num[a]) unionset(num[a], b); //b和a的敌对势力是一伙
if (num[b]) unionset(a, num[b]); //a和b的敌对势力是一伙
num[a] = b;
num[b] = a;
}
else
{
if (findset(a) == findset(num[b])) printf("In different gangs.\n");
else if (findset(a) == findset(b)) printf("In the same gang.\n");
else printf("Not sure yet.\n");
}
}
}
return 0;
}